research project topics mathematics

Home › Study Tips › 100 Ideas for Research Projects in Mathematics

100 Ideas for Research Projects in Mathematics

• Published November 18, 2024

Completing a mathematics research project allows you to explore real-word applications of mathematical concepts. Choosing the right EPQ or dissertation topic could guide you toward a rewarding career in mathematics. So, check out our list of 100 ideas for research projects in mathematics to find inspiration.

What Makes a Great Research Topic in Mathematics?

Ask yourself what would make a great EPQ topic in mathematics for you. As you make your decision, keep these key points in mind:

• Scope: while narrowing down a question allows you to limit the scope, ensure that your topic is broad enough to explore.
• Personal interest: having a personal interest in an EPQ mathematics research project ensures that you remain engaged and motivated throughout. 
• Application: pick an EPQ topic in mathematics that can solve real-world problems and contribute to the field.
• Originality: look to approach your chosen research topic from a unique angle to offer a fresh perspective.

100 Research Ideas for Mathematics

Research project ideas in pure mathematics.

• The mathematics of chaos theory and its applications
• The Fibonacci sequence and its occurrence in nature
• Geometry of fractals and their real-world applications
• Investigating number theory and prime numbers
• What is the Riemann Hypothesis and why is it important?
• Exploring the P vs. NP problem
• The history and development of calculus
• The development and importance of complex numbers in mathematics
• Exploring the importance of rigour in mathematics
• Understanding non-Euclidean geometry and its applications
• Exploring the mathematics of string theory
• Exploring the concept of infinity in mathematics
• The importance of mathematical logic and set theory
• The importance of group theory in abstract algebra
• Investigating the role of algebra in solving equations and systems
• The role of polynomials in solving algebraic equations
• The importance of mathematical proofs in geometry
• Exploring the role of algebraic structures in solving equations
• The role of symmetry in solving algebraic equations
• The use of combinatorics in solving complex problems
• How prime numbers are used in cryptography

Research Project Ideas about Applied Mathematics in Technology and Computing

• The role of mathematics in cryptography
• Using linear algebra to understand 3D transformations in computer graphics
• The mathematics behind machine learning algorithms
• Analysing the mathematics behind search engines
• The role of algorithms in solving Rubik’s cube
• The mathematics behind blockchain technology
• The role of discrete mathematics in computer science
• The role of Monte Carlo methods in probability and statistics
• The use of set theory in computer programming
• Exploring optimisation algorithms in machine learning
• Investigating cryptographic methods based on prime factorisation
• How do algorithms work?
• The mathematics behind artificial neural networks
• The role of geometry in computer vision and image recognition

Research Project Ideas about Mathematics in Physical Sciences and Engineering

• Exploring the mathematics of elliptical curves and their applications
• The mathematics of symmetry in crystallography
• Investigating topology and its application in physics
• The application of differential equations in engineering
• The role of eigenvalues and eigenvectors in physics
• The role of dimensional analysis in physics
• Exploring the mathematics of fluid dynamics
• The mathematics of black holes
• The role of partial differential equations in modelling heat transfer
• The mathematics of flight dynamics
• Exploring how Fourier analysis is used in signal processing
• Investigating the use of calculus in physics
• The application of calculus in electrical engineering
• Investigating how calculus is used in pharmacokinetics
• The use of trigonometry in astronomy
• The role of probability in quantum mechanics
• Knot theory and its applications in biology and chemistry
• Exploring the role of vectors in physics and engineering
• Exploring the applications of matrix theory in quantum physics

Research Project Ideas about Mathematics in Economics and Finance

• Game theory and its applications in economics
• The mathematics behind stock market predictions
• Mathematical optimisation in logistics and supply chains
• The role of mathematics in AI
• Investigating the use of mathematical models in economics
• Bayesian probability and its applications
• The role of stochastic processes in economics
• The applications of linear programming in business optimisation
• The use of statistics in analysing sports performance

Research Project Ideas about Mathematics in Biology and Medicine

• Mathematical models of infectious diseases
• Investigating the role of probability in genetics
• The role of statistics in health and medical research
• The use of mathematical models in epidemiology
• Exploring statistical models in medical research
• Investigating mathematical modelling in sports performance analysis
• The applications of statistics in psychology and social sciences
• The importance of mathematical models in ecology
• Investigating the use of mathematical models in cancer research
• Investigating the mathematics behind disease spread in populations

Research Project Ideas about Mathematics and the Climate

• The mathematics of chaos and weather prediction
• The use of mathematical models in environmental conservation
• How mathematical models are used in predicting natural disasters
• Investigating the use of mathematics in climate modelling

Research Project Ideas about Mathematics and the Humanities

• The mathematics behind traffic optimisation in urban planning
• Exploring the relationship between probability and gambling
• Mathematical models of population growth
• Exploring mathematical approaches to solving traffic flow problems
• The mathematics of traffic optimisation in urban planning
• Exploring the mathematics of social media analysis
• The mathematics behind solving sudoku
• Exploring the applications of graph theory in networks and communications

Research Project Ideas about Mathematics and the Arts

• The mathematics behind architectural design
• The role of mathematics in music theory
• Investigating the golden ratio in art
• The influence of fractals in visual arts
• Exploring symmetry and patterns in art and design

Research Project Ideas about Mathematics and Politics

• How statistics can be used to predict election outcomes
• The mathematics of voting systems
• The use of game theory in political decision-making
• Investigating the mathematics of optical illusions
• Using network theory to understand political alliances

Choose a Motivating Mathematics EPQ Topic Today

Feeling inspired by Immerse Education ’s list of EPQ topic ideas? Mathematics is a diverse field that offers countless research questions for you to explore. It’s essential that you choose the right one that allows you to investigate the area of mathematics that appeals to you.

Visit the Immerse Education Mathematics Online Research Programme Page to take the first step. Here you’ll find expert academics who can guide your research process and inspire a university-level essay on your chosen EPQ topic. 

• I'm a Parent
• I'm a Student
• First Name *
• Last Name *
• Phone number *
• School Country
• School City
• School Name
• School SF ID
• Which subjects interest you? (Optional) Architecture Artificial Intelligence Banking and Finance Biology Biotechnology Business Management Chemistry Coding Computer Science Creative Writing Criminology Economics Encryption and Cybersecurity Engineering English Literature Entrepreneurship Fashion and Design Female Future Leaders Film and Animation Fine and Digital Art Film Studies Global Society and Sustainability History International Relations Law Marketing and Entertainment Mathematics Medicine Medicine and Health Sciences Media and Journalism Nanotechnology Natural Sciences Philosophy Philosophy Politics and Economics Physics Psychology Software Development and AI Software Development and Gaming Veterinary Studies Online Research Programme
• Yes. See Privacy Policy

Secure priority enrolment for our new summer school location with a small refundable deposit.

" * " indicates required fields

Receive priority enrolment for new summer school locations by registering your interest below.

Our programme consultant will contact you to talk about your options.

• Family Name *
• Phone Number
• Yes. See Privacy Policy.

Subject is unavailable at location

You have selected a subject that is not available at the location that you have previously chosen.

The location filter has been reset, and you are now able to search for all the courses where we offer the subject.

• Write my thesis
• Thesis writers
• Buy thesis papers
• Bachelor thesis
• Master's thesis
• Thesis editing services
• Thesis proofreading services
• Buy a thesis online
• Write my dissertation
• Dissertation proposal help
• Pay for dissertation
• Custom dissertation
• Dissertation help online
• Buy dissertation online
• Cheap dissertation
• Dissertation editing services
• Write my research paper
• Buy research paper online
• Pay for research paper
• Research paper help
• Order research paper
• Custom research paper
• Cheap research paper
• Research papers for sale
• Thesis subjects
• How It Works

181 Mathematics Research Topics From PhD Experts

If you are reading this blog post, it means you are looking for some exceptional math research topics. You want them to be original, unique even. If you manage to find topics like this, you can be sure your professor will give you a top grade (if you write a decent paper, that is). The good news is that you have arrived at just the right place – at the right time. We have just finished updating our list of topics, so you will find plenty of original ideas right on this page. All our topics are 100 percent free to use as you see fit. You can reword them and you don’t need to give us any credit.

And remember: if you need assistance from a professional, don’t hesitate to reach out to us. We are not just the best place for math research topics for high school students; we are also the number one choice for students looking for top-notch research paper writing services.

Our Newest Research Topics in Math

We know you probably want the best and most recent research topics in math. You want your paper to stand out from all the rest. After all, this is the best way to get some bonus points from your professor. On top of this, finding some great topics for your next paper makes it easier for you to write the essay. As long as you know at least something about the topic, you’ll find that writing a great paper or buy phd thesis isn’t as difficult as you previously thought.

So, without further ado, here are the 181 brand new topics for your next math research paper:

Cool Math Topics to Research

Are you looking for some cool math topics to research? We have a list of original topics for your right here. Pick the one you like and start writing now:

• Roll two dice and calculate a probability
• Discuss ancient Greek mathematics
• Is math really important in school?
• Discuss the binomial theorem
• The math behind encryption
• Game theory and its real-life applications
• Analyze the Bernoulli scheme
• What are holomorphic functions and how do they work?
• Describe big numbers
• Solving the Tower of Hanoi problem

Undergraduate Math Research Topics

If you are an undergraduate looking for some research topics for your next math paper, you will surely appreciate our list of interesting undergraduate math research topics:

• Methods to count discrete objects
• The origins of Greek symbols in mathematics
• Methods to solve simultaneous equations
• Real-world applications of the theorem of Pythagoras
• Discuss the limits of diffusion
• Use math to analyze the abortion data in the UK over the last 100 years
• Discuss the Knot theory
• Analyze predictive models (take meteorology as an example)
• In-depth analysis of the Monte Carlo methods for inverse problems
• Squares vs. rectangles (compare and contrast)

Number Theory Topics to Research

Interested in writing about number theory? It is not an easy subject to discuss, we know. However, we are sure you will appreciate these number theory topics:

• Discuss the greatest common divisor
• Explain the extended Euclidean algorithm
• What are RSA numbers?
• Discuss Bézout’s lemma
• In-depth analysis of the square-free polynomial
• Discuss the Stern-Brocot tree
• Analyze Fermat’s little theorem
• What is a discrete logarithm?
• Gauss’s lemma in number theory
• Analyze the Pentagonal number theorem

Math Research Topics for High School

High school students shouldn’t be too worried about their math papers because we have some unique, and quite interesting, math research topics for high school right here:

• Discuss Brun’s constant
• An in-depth look at the Brahmagupta–Fibonacci identity
• What is derivative algebra?
• Describe the Symmetric Boolean function
• Discuss orders of approximation in limits
• Solving Regiomontanus’ angle maximization problem
• What is a Quadratic integral?
• Define and describe complementary angles
• Analyze the incircle and excircles of a triangle
• Analyze the Bolyai–Gerwien theorem in geometry
• Math in our everyday life

Complex Math Topics

If you want to give some complex math topics a try, we have the best examples below. Remember, these topics should only be attempted by students who are proficient in mathematics:

• Mathematics and its appliance in Artificial Intelligence
• Try to solve an unsolved problem in math
• Discuss Kolmogorov’s zero-one law
• What is a discrete random variable?
• Analyze the Hewitt–Savage zero-one law
• What is a transferable belief model?
• Discuss 3 major mathematical theorems
• Describe and analyze the Dempster-Shafer theory
• An in-depth analysis of a continuous stochastic process
• Identify and analyze Gauss-Markov processes

Easy Math Research Paper Topics

Perhaps you don’t want to spend too much time working on your next research paper. Who can blame you? Check out these easy math research paper topics:

• Define the hyperbola
• Do we need to use a calculator during math class?
• The binomial theorem and its real-world applications
• What is a parabola in geometry?
• How do you calculate the slope of a curve?
• Define the Jacobian matrix
• Solving matrix problems effectively
• Why do we need differential equations?
• Should math be mandatory in all schools?
• What is a Hessian matrix?

Logic Topics to Research

We have some interesting logical topics for research papers. These are perfect for students interested in writing about math logic. Pick one right now:

• Discuss the reductio ad absurdum approach
• Discuss Boolean algebra
• What is consistency proof?
• Analyze Trakhtenbrot’s theorem (the finite model theory)
• Discuss the Gödel completeness theorem
• An in-depth analysis of Morley’s categoricity theorem
• How does the Back-and-forth method work?
• Discuss the Ehrenfeucht–Fraïssé game technique
• Discuss Aleph numbers (Aleph-null and Aleph-one)
• Solving the Suslin problem

Algebra Topics for a Research Paper

Would you like to write about an algebra topic? No problem, our seasoned writers have compiled a list of the best algebra topics for a research paper:

• Discuss the differential equation
• Analyze the Jacobson density theorem
• The 4 properties of a binary operation in algebra
• Analyze the unary operator in depth
• Analyze the Abel–Ruffini theorem
• Epimorphisms vs. monomorphisms: compare and contrast
• Discuss the Morita duality in algebraic structures
• Idempotent vs. nilpotent in Ring theory
• Discuss the Artin-Wedderburn theorem
• What is a commutative ring in algebra?
• Analyze and describe the Noetherian ring

Math Education Research Topics

There is nothing wrong with writing about math education, especially if your professor did not give you writing prompts. Here are some very nice math education research topics:

• What are the goals a mathematics professor should have?
• What is math anxiety in the classroom?
• Teaching math in UK schools: the difficulties
• Computer programming or math in high school?
• Is math education in Europe at a high enough level?
• Common Core Standards and their effects on math education
• Culture and math education in Africa
• What is dyscalculia and how does it manifest itself?
• When was algebra first thought in schools?
• Math education in the United States versus the United Kingdom

Computability Theory Topics to Research

Writing about computability theory can be a very interesting adventure. Give it a try! Here are some of our most interesting computability theory topics to research:

• What is a multiplication table?
• Analyze the Scholz conjecture
• Explain exponentiating by squaring
• Analyze the Myhill-Nerode theorem
• What is a tree automaton?
• Compare and contrast the Pushdown automaton and the Büchi automaton
• Discuss the Markov algorithm
• What is a Turing machine?
• Analyze the post correspondence problem
• Discuss the linear speedup theorem
• Discuss the Boolean satisfiability problem

Interesting Math Research Topics

We know you want topics that are interesting and relatively easy to write about. This is why we have a separate list of our most interesting math research topics:

• What is two-element Boolean algebra?
• The life of Gauss
• The life of Isaac Newton
• What is an orthodiagonal quadrilateral?
• Tessellation in Euclidean plane geometry
• Describe a hyperboloid in 3D geometry
• What is a sphericon?
• Discuss the peculiarities of Borel’s paradox
• Analyze the De Finetti theorem in statistics
• What are Martingales?
• The basics of stochastic calculus

Applied Math Research Topics

Interested in writing about applied mathematics? Our team managed to create a list of awesome applied math research topics from scratch for you:

• Discuss Newton’s laws of motion
• Analyze the perpendicular axes rule
• How is a Galilean transformation done?
• The conservation of energy and its applications
• Discuss Liouville’s theorem in Hamiltonian mechanics
• Analyze the quantum field theory
• Discuss the main components of the Lorentz symmetry
• An in-depth look at the uncertainty principle

Geometry Topics for a Research Paper

Geometry can be a very captivating subject, especially when you know plenty about it. Check out our list of geometry topics for a research paper and pick the best one today:

• Most useful trigonometry functions in math
• The life of Archimedes and his achievements
• Trigonometry in computer graphics
• Using Vincenty’s formulae in geodesy
• Define and describe the Heronian tetrahedron
• The math behind the parabolic microphone
• Discuss the Japanese theorem for concyclic polygons
• Analyze Euler’s theorem in geometry

Math Research Topics for Middle School

Yes, even middle school children can write about mathematics. We have some original math research topics for middle school right here:

• Finding critical points in a graph
• The basics of calculus
• What makes a graph ultrahomogeneous?
• How do you calculate the area of different shapes?
• What contributions did Euclid have to the field of mathematics?
• What is Diophantine geometry?
• What makes a graph regular?
• Analyze a full binary tree

Math Research Topics for College Students

As you’ve probably already figured out, college students should pick topics that are a bit more complex. We have some of the best math research topics for college students right here:

• What are extremal problems and how do you solve them?
• Discuss an unsolvable math problem
• How can supercomputers solve complex mathematical problems?
• An in-depth analysis of fractals
• Discuss the Boruvka’s algorithm (related to the minimum spanning tree)
• Discuss the Lorentz–FitzGerald contraction hypothesis in relativity
• An in-depth look at Einstein’s field equation
• The math behind computer vision and object recognition

Calculus Topics for a Research Paper

Let’s face it: calculus is not a very difficult field. So, why don’t you pick one of our excellent calculus topics for a research paper and start writing your essay right away:

• When do we need to apply the L’Hôpital rule?
• Discuss the Leibniz integral rule
• Calculus in ancient Egypt
• Discuss and analyze linear approximations
• The applications of calculus in real life
• The many uses of Stokes’ theorem
• Discuss the Borel regular measure
• An in-depth analysis of Lebesgue’s monotone convergence theorem

Simple Math Research Paper Topics for High School

This is the place where you can find some pretty simple topics if you are a high school student. Check out our simple math research paper topics for high school:

• The life and work of the famous Pierre de Fermat
• What are limits and why are they useful in calculus?
• Explain the concept of congruency
• The life and work of the famous Jakob Bernoulli
• Analyze the rhombicosidodecahedron and its applications
• Calculus and the Egyptian pyramids
• The life and work of the famous Jean d’Alembert
• Discuss the hyperplane arrangement in combinatorial computational geometry
• The smallest enclosing sphere method in combinatorics

Business Math Topics

If you want to surprise your professor, why don’t you write about business math? We have some exceptional topics that nobody has thought about right here:

• Is paying a loan with another loan a good approach?
• Discuss the major causes of a stock market crash
• Best debt amortization methods in the US
• How do bank loans work in the UK?
• Calculating interest rates the easy way
• Discuss the pros and cons of annuities
• Basic business math skills everyone should possess
• Business math in United States schools
• Analyze the discount factor

Probability and Statistics Topics for Research

Probability and statistics are not easy fields. However, you can impress your professor with one of our unique probability and statistics topics for research:

• What is the autoregressive conditional duration?
• Applying the ANOVA method to ranks
• Discuss the practical applications of the Bates distribution
• Explain the principle of maximum entropy
• Discuss Skorokhod’s representation theorem in random variables
• What is the Factorial moment in the Theory of Probability?
• Compare and contrast Cochran’s C test and his Q test
• Analyze the De Moivre-Laplace theorem
• What is a negative probability?

Need Help With Research Paper?

We offer the absolute best high school and college research paper writing service on the Internet. When you need any kind of research paper help, our experienced ENL writers and professional editors are here to help. With years of experience under their belts, our experts can get your research paper done in as little as 3 hours.

Getting cheap online help with research papers has never been easier. College students should just get in touch with us and tell us what they need. We will assign them our most affordable and experienced math writer in minutes, even during the night. We are the best-rated online writing company on the Internet because we always deliver high-quality academic content at the most competitive prices. Give us a try today!

Leave a Reply Cancel reply

12 Math Project Ideas for Middle and High School Students

By János Perczel

Co-founder of Polygence, PhD from MIT

7 minute read

The mathematician Eric Temple Bell wrote that “‘Obvious’ is the most dangerous word in mathematics.” What he meant is that a lot of math focuses on scrutinizing and challenging our intuitions. In other words, just because something seems obvious doesn’t necessarily make it true. In fact, the “obvious” is often false. That’s a powerful idea that can be exciting to some students and, simultaneously, a little bit terrifying to others. If the idea of using logic to interrogate intuition lights a spark in your inquisitive brain, then you may want to explore your passion for math!

Mathematics serves as the foundation for most fields of science, such as physics, engineering, computer science, and economics. It equips you with critical problem-solving skills and the ability to break down complex problems into smaller, more manageable parts. It helps you avoid ambiguity and communicate in what is often called “the universal language,” so-called because its principles and concepts are the same worldwide. Beyond the fact that studying math can open up many career opportunities, some mathematicians also simply find beauty in the equations and proofs themselves.

How do I find my math passion project focus?

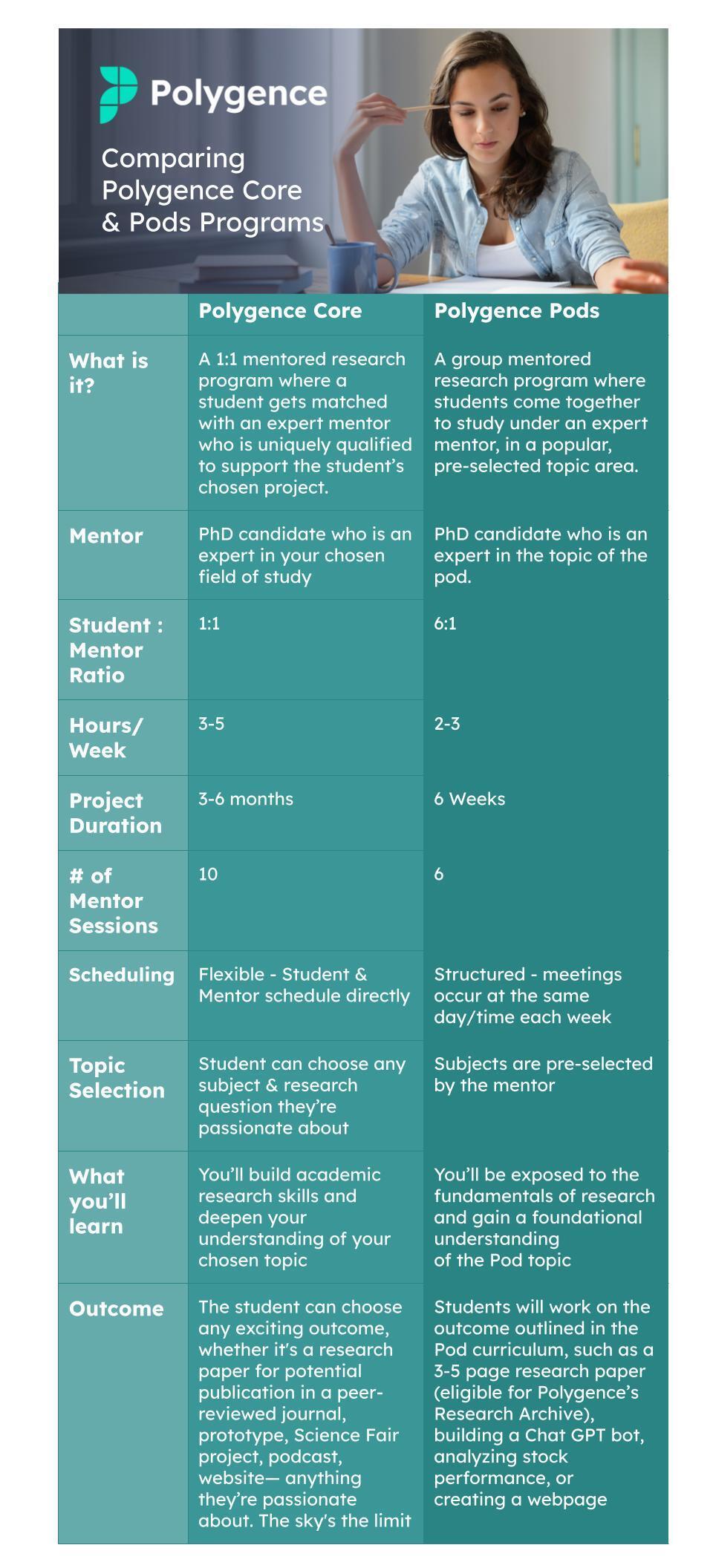
If you're passionate about math and seeking a creative project, consider joining our Polygence Pods program. This unique opportunity brings together small groups of 3-6 like-minded high school students with a world-class expert to explore complex mathematical problems. Over six weekly sessions, you'll collaborate on a group project focused on a specific math-related subject. Whether you're interested in sports statistics, data visualization for endangered species habitats, or the physical manifestations of mathematical concepts, there's a Pod for you. 

Because math is so foundational in the sciences, there are many different directions you can take with your math passion project. Decide which topics within mathematics most speak to you. Maybe you’re more interested in how math is used in sports statistics , how you can harness math to visualize data on the habitats of endangered species , or perhaps you’re curious about how math manifests itself in the physical realm . Once you find a topic that interests you, then you can begin to dive deeper.

Keep in mind that some passion projects may require more technical skills, such as computer programming, whereas others may just explore theoretical concepts. The route you take is totally up to you and what you feel comfortable with, but don’t be afraid to join a project if you don’t currently have the technical skills for it. You can view it as an opportunity to learn new skills while also exploring a topic you’re excited about.

Do your own research through Polygence!

Polygence pairs you with an expert mentor in your area of passion. Together, you work to create a high quality research project that is uniquely your own.

What are the best math project ideas?

1. the mathematical properties of elections.

In recent years, there has been a lot of discussion about which election mechanism is most effective at achieving various goals. Proposed mechanisms in United States elections include majority elections, the electoral college, approval voting, and ranked-choice voting. All of these mechanisms have benefits and drawbacks, and it turns out that no perfect election mechanism exists. Look at the work being done by mathematicians to understand when elections fail, and what can be done to improve them. Choose the strongest mechanism and use evidence to support your claim.

Idea by math research mentor Grayson

2. Knot theory

A knot is simply a closed loop of string. Explore how mathematicians represent knots on a page. Learn how knots can be combined, and how to find knots that can't be created by combining other knots. You can learn techniques for determining whether or not two knots are distinct, in the sense that neither can be deformed to match the other. You can also study related objects, such as links and braids, and research the application of knots in the physical sciences.

Idea by math research mentor Alex

3. Bayesian basketball win prediction system

The Bayes’ Rule is crucial to modern statistics (as well as data science and machine learning). Using a Bayesian model to predict the probability distribution of basketball performance statistics, you can attempt to predict a team’s win and loss rate versus another team by drawing samples from these distributions and computing correlation to win or loss. Your project could be as simple or as complicated as you want. Based on your interest and comfort level, you could use simple normal models, mixture models, Gibbs sampling , and hidden Markov models. You can also learn how to code a fairly simple simulation in R or Python. Then, you’ll need to learn how to interpret the significance of statistical results and adjust results over time based on the success/failure of your model over time.

Idea by math research mentor Ari

4. Finding value in Major League Baseball free agency

Here’s another sports-related project idea. Every offseason, there are hundreds of professional baseball players who become free agents and can be signed by any team. This project involves determining which players might be a good "value" by deciding which statistics are most important to helping a team win relative to how players are generally paid. After deciding which stats are the most important, a ranked list of "value" can be produced based on expected salaries.

Idea by math research mentor Dante

5. Impact of climate change on drought risk

Are you interested in environmental economics, risk analysis, or water resource economics?

You can use historical data on precipitation, temperature, soil moisture, drought indicators, and meteorological models that simulate atmospheric conditions to train a machine-learning model that can assess the likelihood and intensity of droughts in different regions under different climate scenarios. You can also explore your assessments' potential adaptation strategies and policy implications. This project would require some skills in data processing, machine learning, and meteorological modeling.

Idea by math research mentor Jameson

Go beyond crunching numbers

Interested in Math? We'll match you with an expert mentor who will help you explore your next project.

6. Making machines make art 

You can program a computer to create an infinite number of images, music, video game levels, 3D objects, or text using techniques like neural style transfer, genetic algorithms, rejection sampling, Perlin noise , or Voronoi tessellation . Your challenge then is to create a functioning content generator that you could then showcase on a website, research conference, or even in a gallery exhibition.

Idea by math research mentor Sam

7. Measuring income inequality and social mobility

If you’re interested in the intersection of mathematics and public policy, here’s an idea. Use data from the World Bank, the Organization for Economic Co-operation and Development (OECD), and other sources to calculate the Gini coefficient and the intergenerational elasticity of income for different countries and regions over time. Explore the factors that influence these measures and their implications for economic development and social justice. You will need to have some skills in data collection, analysis, and visualization.

8. Rocket (fuel) science

Rockets are mainly made out of fuel. When the fuel burns, it gets heated and expelled out, producing thrust. Fuel is heavy and, for long-range space missions, we need to carry around the fuel for the rest of the mission the whole way. It is important that the fuel gives us the most bang for our buck (i.e., the most acceleration per unit of fuel). Compare the amount of fuel (weight) required to get to various celestial objects and back using current electric and chemical propulsion technologies . Then do a cost analysis and compare how long it would take.

Idea by math research mentor Derek

9. COVID-19 and the global financial crisis

It is shocking how the economic effects of COVID-19 have far outweighed the ones from the Global Financial Crisis in 2007-08 . How much is the difference in terms of employment? Production? Let's go to the data!

Idea by math research mentor Alberto

10. Modeling polarization in social networks

We've all seen or heard about nasty political arguments and echo chambers on social media, but how and why do these happen? To try and find out, construct a mathematical and/or computational model of how people with different opinions interact in a social network. When do people come to a consensus, and when do they become more strongly divided? How can we design social networks with these ideas in mind?

Idea by math research mentor Emily

11. The world of mathematics

The history of mathematics dates all the way back to the very first civilizations and followed throughout history all over the globe. This development leads us to our way of living and thinking today. Rarely taught in math courses, the origins of math can provide clear insight into the necessities of learning math and the broad applications that math has in the world. Conduct research on a chosen time period, location, or figure in mathematics and describe the impacts this innovation or innovator had on the development of math as we know it today.

Idea by math research mentor Shae

12. Simulating the stock market

Here’s an idea for a beginner-to-intermediate statistics and programming project centered around Monte Carlo simulations. Monte Carlo simulations are random methods for modeling the outcome of a complicated process. These methods are used in finance all the time. How could you code a program that uses the Monte Carlo technique to "simulate" the stock market? You will need some familiarity with statistics, basic finance, and basic programming in any language to complete this project.

Idea by math research mentor Sahil

How can I showcase my math project?

After you’ve done the hard work of completing your mathematics passion project, it’s also equally important to showcase your accomplishments . You can see that in many of the project ideas above, there is a clear topic, but how you want to present the project is open-ended. You could try to publish a research paper , create a podcast or infographic, or even create a visual representation of your concept. You’ll find that although many project ideas can simply be summarized in a paper, projects can also be showcased in other creative ways.

Polygence Scholars Are Also Passionate About

What are some examples of math passion projects completed by polygence students.

There are several examples of math projects Polygence students have completed through enrolling in our programs; we’ll highlight two here.

Ahmet's mathematical passion project offers detailed breakdowns of the first introduced quantum algorithm Deutsch-Jozsa, and the first quantum algorithm proven to be faster than classical algorithms, Grover’s Algorithm. It also includes a side-by-side comparison of the quantum algorithms and their classical counterparts. He uploaded his paper on Github and plans to submit it to an official publication soon.

Anna’s finance project provides an overview of topics related to personal finance, covering tax and benefits, tax-deferred savings, interest rates, cost of living, investing, insurance, and housing to help young adults manage their savings. To further her understanding of how different areas of finance influence one's life consumption, she created a life consumption plan for a hypothetical person and produced a paper. 

View more passion project ideas for high school students .

How can I get guidance and support on my math project?

In this post, we covered how to find the right mathematics project for you and discussed how to showcase your project. If you’re also curious about research projects in other subjects, check out our ideas for physics projects and music projects for high school students.

If you have a passion for math–or are generally curious about exploring mathematical concepts–and are interested in pursuing a passion project, Polygence Pods is the perfect place to start. Pods are flexible and personalized learning environments that offer students all of the benefits of expert guidance in the context of a small, supportive, and collaborative group. They are especially well-suited to students who want to explore or deepen their academic interests through a focused and structured research experience, and who also enjoy learning alongside a handful of like-minded peers. Sessions blend interactive lectures with dynamic group discussions in which students are asked to challenge their intuitions. While Pod sessions bring the group together, each student in the group is encouraged to produce an individual research outcome.

Ready to challenge the “obvious”? Polygence’s Pods program is ready to help you plunge into a theoretical or practical research experience guided by mathematics and a world-class mathematical mentor.

220 Brilliant Math Research Topics and Ideas for Students

Table of Contents

Do you have to submit a math research paper? Are you looking for the best math research topics? Well, in this blog post, we have shared a list of 220 interesting math research topics to consider for assignments and academic projects. If you are a student who is pursuing a degree in mathematics, then you can very well use the topic ideas suggested here. Also, you can check this blog post and get to know the important steps for writing a brilliant math research paper.

What is Mathematics?

Mathematics is a broad academic discipline that focuses on numbers, structures, spaces, and shapes. This subject contains many analysis and calculation methods. Especially in the real world, math is considered an effective problem-solving tool. By using math, you can find solutions for both simple and complex problems.

Mathematics is an integrated language that is widely used in several fields such as engineering, physics, medicine, finance, computer, business, and biology. Apart from the complex scientific fields, even math plays a vital role in the basic cost and time calculation in our everyday lives.

Different Branches of Mathematics

Listed below are some popular branches of mathematics.

Arithmetic: It is a basic branch of math that focuses on numbers and their associated operations such as addition, subtraction, multiplication, and division.

Algebra: When the numbers are unknown, algebra steps in. Generally, along with numbers, algebra uses the letters such as A, B, X, and Y to represent unknown quantities. Mainly, businesses depend on algebra concepts to predict their sales.

Geometry: It is a popular branch of mathematics that deals with shapes, sizes, and figures. The concept commonly revolves around lines, points, solids, angles, and surfaces.

Apart from all these common branches, mathematics also includes more advanced types such as calculus, trigonometry, statistics, topology, probability, etc.

How to Write a Math Research Paper

In general, a math research paper is an academic paper that is prepared to explain a mathematical concept with proper results. For writing a math research paper, first, you must have a good research topic from any branch of mathematics. As math is a vast discipline, you can easily search and find plenty of research topics from it. But when you have many topics, then it will be more tedious to identify one perfect topic out of them all.

Right now, are you searching for a perfect math research topic? Well, then this is what you should do during the topic selection process to spot the right topic.

Topic Selection

Whenever you are asked to come up with a research paper topic on your own, initially, restrict yourself to the research area that you have strong knowledge of and are passionate about. Next, in that research area, explore and identify one great topic that has a broad scope to evaluate and express your ideas.

Remember, the topic you select should be comfortable for you to perform research and write about. Never pick a topic with less or no research scope. The topic should support the research method of your choice. Most importantly, give preference to the topic that has wide research information, references, and evidence. Also, before finalizing the topic, check whether your topic satisfies your instructor’s guidelines.

Research Paper Writing

After you have found a good math research topic, you can proceed to write the research paper. The research paper you write should follow a proper format and structure. So, in the math research paper, make sure to include the following essential sections.

Introduction

Implications.

In the introduction section, you should first give brief background information about your topic to familiarize your readers. Here, mainly you should explain the primary concepts along with the history of its terms. Also, you should state the basic research problem and discuss the symbols and principles that you are going to use in the essay.

The body of your research paper should elaborate on all your findings. Particularly, in the body paragraphs, you should talk about the formulas, theories, and mathematical analysis methods you have used to find solutions for the research problem.

The implication is the last or closing part of your research paper. Here, you should share your research insights with the readers. Also, you should include a summary of all the important points that you have discussed in the entire essay.

Tips for Choosing a Good Math Research Topic

It might be confusing for you to identify a good topic for your math research paper, but by following these tips you can spot the appropriate topic for your study.

• Identify which area in mathematics you are interested in and then pick a topic relevant to it. For instance, you may perform math research on topics from areas such as number theory, geometry, algebra, and so on.
• To generate math research paper topics, look for open problems or conjectures in math journals, conferences, or online forums.
• Select a math research topic that is doable and has sufficient resources for the study.
• Give preference to math research ideas that have a close connection with other fields or any real-world applications.
• If the topic you have chosen is broad, narrow it down. Always focus on a specific research topic or a question with a good scope for discussion and analysis.
• Make sure the math research topic you have selected is original and can be approached from a fresh perspective
• Discuss your math research idea with professors, researchers, or classmates and then obtain their insight and feedback. This will help you refine your idea and come up with high-quality work.

List of the Best Math Research Topics

Are you struggling to come up with a good math research paper topic for your assignment? No worries! Here we have shared a list of top-rated math research topic ideas on various branches of mathematics.

Explore them all and find a topic that suits you perfectly.

Simple and Easy Math Topics

If you want to perform math research effortlessly, then take into account any of the topics based on the fundamental concepts of mathematics rather than complex ideas. Listed below are a few simple math study topics that will be easy for you to examine.

• Explain the working of Partial fractions.
• Discuss the application of Mathematics in daily life.
• What is the basis of Cramer’s rule?
• How to solve Heesch’s problem?
• Explain the history of calculus .
• What is Euler’s formula?
• Explain the working of Logarithms.
• What are the different types of sequences?
• Explain the different types of Transformations.
• Define Brun’s constant.
• What are the methods of factoring quadratics?
• Examine Archimedean solids.
• Explain Gaussian elimination.
• Write about encryption and prime numbers.
• How does Hypercube work?
• Analyze Pygaoethores Theorem
• Describe the logicist definitions of mathematics
• Describe the purpose of homological algebra
• Compare and contrast Concave and Convex in geometry
• The study and contributions of Blaise Pascal to Probability
• Explain the Fibonacci series briefly
• How the Ancient Greek architecture influenced by mathematics?
• Discuss the ancient Egyptian mathematical applications and accomplishments
• Discuss the easiest ways to memorize algebraic expressions
• Algebra is an exposition on the invariants of matrices – Explain

Basic Math Topics for Middle School Students

Do you need math research topics for middle school students? Take a look below. In the list, we have suggested some fascinating research topics on mathematics for middle school students to get started.

• Define the Artin-Wedderburn theorem.
• How to calculate net worth?
• How to identify critical points in graphs?
• What is the role of statistics in business?
• Describe the principles of the Pythagoras theorem.
• What are the applications of finance in math?
• What do limits in math mean?
• Explain the ratio and root test.
• Define Jacobson’s density theorem.
• What are the principles of calculus?

Interesting Math Topics for High School Students

If it is challenging for you to identify a good math research topic for your high school assignment, make use of the list published here. For high school students, we have provided some interesting math research questions in the list to explore.

• What are the different number types? Explain with examples.
• Explain the need for imaginary numbers.
• How to calculate the interest rate?
• How to solve a matrix?
• How to prepare a chart of a company’s financial analysis?
• When to use a calculator in class?
• Explain the importance of the Binomial theorem.
• Write about Egyptian mathematics.
• Describe the applications of math in the workplace.
• How to solve linear equations?
• Describe the usage of hyperbola in math.
• Why do so many students hate math?
• What is the difference between algebra and arithmetic?
• How to calculate the mean value?
• What is the numerical data?

Math Research Paper Topics for Undergraduate Students

Are you an undergraduate student searching for math research ideas? Get help from the list uploaded below. To make the topic selection easier for students, in the list, we have added some exclusive research paper topics and ideas on different math disciplines.

• Explain the different theories of mathematical logic.
• Discuss the origins of Greek symbols in mathematics.
• Explain the significance of circles.
• Analyze predictive models.
• Explain the emergence of patterns in chaos theory.
• Define abstract algebra.
• What is a continuous stochastic process?
• Write about the history of algebra.
• Analyze Monte Carlo methods for inverse problems.
• What are the goals of standardized testing?
• Define the Pentagonal number theorem.
• Discuss the Lorentz–FitzGerald contraction hypothesis in relativity.
• How to solve simultaneous equations.
• How do supercomputers solve complex mathematical problems?
• What is a parabola in geometry?

Math Research Topics for College Students

In this section, we have provided a list of incredible math research topics for college students. If you require a perfect math research topic for your college assignment, from the list, choose any study topic that aligns with your needs and explore it extensively.

• Explain the Fibonacci sequence.
• What are the core problems of computational geometry?
• Discuss the practical applications of game theory.
• What is the Traveling Salesman Problem?
• Describe the Influence of math in biology.
• Analyze the meaning of fractals.
• Discuss the origin and evolution of mathematics.
• What is quantum computing?
• Explain Einstein’s field equation theory.
• What is the influence of math on chemistry?
• How to solve a Rubik’s cube mathematically?
• How to do complex numbers division?
• Explain the use of Boolean functions.
• Analyze the degrees in polynomial functions.
• How to solve Sudoku using mathematics?
• Explain the use of set theory.
• Explain the math behind the Koch snowflake.
• Explore the varieties of the Tower of Hanoi solutions.
• What is the difference between a discrete and a continuous probability distribution?
• How does encryption work?

Applied Math Research Topics

Applied Mathematics is the practical application of mathematical principles to solve real-world issues in domains such as physics, engineering, and economics. If you wish to explore practical issues in your math research paper, then you may work on any of the below-listed applied math study topics.

• What is the role of algorithms in probabilistic modeling?
• Explain the significance of step-stress modeling.
• Describe Newton’s laws of motion.
• What dimensions are used to examine fingerprints?
• Analyze statistical signal processing.
• How to do Galilean transformation?
• What is the role of mathematicians in crime data analysis and prevention?
• Explain the uncertainty principle.
• Discuss Liouville’s theorem in Hamiltonian mechanics.
• Analyze the perpendicular axes rule.

Business Math Research Topics

Business Math typically focuses on the mathematical principles and methods used to analyze and solve problems in finance, accounting, and management. In case, you are passionate about finance-related things, then in your research paper, you may investigate any of these business math topics.

• What is the difference between a loan and a mortgage?
• How to calculate sales tax?
• Explore the math behind debt amortization.
• How do businesses use statistics?
• What is the economic lot scheduling problem?
• Explain how loans work.
• Discuss the significance of business math in real life.
• Define discount factor.
• What are the major causes of a stock market crash?
• Compare the uses of different types of charts.
• Describe the notions of markups and markdowns.
• How does critical path analysis work?
• What are the pros and cons of annuities?
• When to use multi-period models?
• Compare business and consumer math.

Advanced Math Research Paper Topics

In your math research paper, you may examine and write about any of the below-listed advanced math topics. Calculus, differential equations, and number theory are some examples of advanced mathematical principles used in specific domains.

• What is an oblivious transfer?
• Compare the Riemann and the Ruelle zeta functions.
• What are the different types of knapsack problems?
• Define an abelian group.
• What are the algorithms used for machine learning?
• Define various cases of algebraic cycles.
• When a trigonometric series is called a Fourier series?
• What is the minimum overlap problem?
• What are the basic properties of holomorphic functions?
• Describe the Bernoulli scheme.

Complex Math Research Topics

Complex Math is the study of mathematical structures including non-real numbers such as complex analysis and complex geometry. Listed below are a few complex math study topics you may investigate in your mathematics research paper.

• Write about Napier’s bones.
• What makes a number big?
• Examine the notion of operator spaces.
• How do barcodes function?
• Define Fisher’s fundamental theorem of natural selection.
• What are the peculiarities of Borel’s paradox?
• How to design a train schedule for a whole country?
• Describe a hyperboloid in 3D geometry.
• What is an orthodiagonal quadrilateral?
• Explain how the Iwasawa theory relates to modular forms.

Math Research Ideas on Probability and Statistics

Probability and Statistics focus on the study of chance events, data analysis, and inference for making educated judgments. Here are some amazing research questions on probability and statistics you may examine in your math thesis.

• Roll two dice and calculate a probability.
• Write about the Factorial moment in the Theory of Probability.
• Explain the principle of maximum entropy.
• Compare and contrast Cochran’s C test and his Q test.
• Discuss Skorokhod’s representation theorem in random variables
• How to apply the ANOVA method to rank.
• Analyze the De Moivre-Laplace theorem.
• What is the autoregressive conditional duration?
• Explain a negative probability.
• Discuss the practical applications of the Bates distribution.

Algebra Research Topics

Algebra deals with the study of variables, equations, and functions used to solve systems and model relationships. If you are fascinated by numbers, then for your math research, you may choose any of the below-listed study topics on algebra.

• Explain Descartes’ Rule of Signs.
• How to factor quadratics?
• What is the use of F-algebras?
• Discuss the differential equation.
• What is the difference between eigenvectors and eigenvalues?
• What are the properties of a binary operation in algebra?
• What is a commutative ring in algebra?
• Discuss the origin of the distance formula.
• Explain the quadratic formula.
• Analyze the unary operator.
• Define range and domain in algebra.
• Describe the Noetherian ring.
• Discuss the Morita duality in algebraic structures.
• Define the Abel–Ruffini theorem.
• What is the use of determinants?

Math Research Paper Topics on Geometry

Geometry is the study of object shapes, sizes, and placements, with a focus on qualities and relationships. In case, you are curious about examining shapes and sizes, then in your math research paper, you may address any of these geometry topics.

• Research the real-life uses of a rhombicosidodecahedron.
• Find out the solutions to Buffon’s needle problem.
• What is unique about right triangles?
• What is the Klein bottle?
• What are the Archimedean solids?
• What does congruency mean?
• Discuss the role of trigonometry in computer graphics.
• What is the need for n-dimensional vectors?
• Explain the Japanese theorem for concyclic polygons.
• Prove the angle bisector theorem.
• Identify the applications for the golden ratio.
• Explain the Heronian tetrahedron.
• Describe the notion of Dirac manifolds.
• What is the use of geometry in Picasso’s paintings?
• How do CT scans relate to geometry?

Calculus Research Topics

Calculus studies the rates of change and accumulation, including differential and integral calculus. When it comes to preparing your math research paper, take into consideration any of the below-suggested topics on calculus.

• How to calculate the Taylor series of a function?
• What is the role of calculus in real life?
• Discuss the Leibniz integral rule
• Discuss and analyze linear approximations.
• What is the use of predicate calculus?
• What is the foundation of calculus?
• How to calculate the area between curves?
• Describe the standard formulas needed for derivatives.
• Explain the working of multivariate calculus.
• Define the fundamental theorem of calculus.

Popular Math Research Topics

To prepare your math research paper, take into account any of the below-listed popular study topics. But when you examine a topic that has been commonly chosen by others, analyze it from various dimensions and come up with optimized solutions.

• What is a sphericon?
• What is the role of Mathematics in Artificial Intelligence?
• Define De Finetti’s theorem in probability and statistics.
• How to calculate the slope of a curve?
• Discuss the Stern-Brocot tree.
• Explain Pascal’s Triangle.
• Analyze the Georg Cantor set theory.
• How to measure infinity?
• Explain the Scholz conjecture.
• How is geometry used in contemporary architectural designs?
• How to solve the Suslin problem?
• What is a tree automaton?
• Explain the working of the Back-and-forth method.
• What is a Turing machine?
• Discuss the linear speedup theorem.
• Discuss the benefits of using truth tables to present the logical validity of a propositional expression
• Critical analysis of the major concepts in ancient Egyptian mathematics
• Discuss the similarities and differences between a continuous and a discrete probability distribution
• Analysis of the problem with the wholeness axiom and Kunen’s inconsistency theorem
• Develop a study focusing on the Seven Bridges of Königsberg and relate the problem to the city or state of your choice

Latest Math Research Topics

Listed below are some trending research ideas on mathematics you may consider for your studies. By preparing math research papers on the latest topics or real-world problems, you may promote innovation, advance mathematical knowledge, and drive progress in various associated fields.

• What does point zero reflect on a graph where the vertical and horizontal lines meet?
• How to recognize adjacent angles easily without any trouble?
• Compare the differential vs. analytic geometry by citing relevant examples.
• Explain how to use a graphics system for solving various types of equations.
• How to divide the feasible and non-feasible regions in linear programming?
• What are confidence intervals and how it help in statistical math?
• How to differentiate the effect of a magnetic field on a given point of the circle by using an appropriate differential formula?
• What are the different types of identities that are used in trigonometric functions?
• Why polynomials are difficult to solve as compared to monomials? Give examples.
• Explain radical expressions and their significance with examples.
• Explain how fractal geometry can be used to model natural phenomena.
• Discuss the underlying patterns in prime number distribution.
• How can machine learning be optimized using mathematical techniques?
• What new cryptographic algorithms can be developed using number theory?
• What combinatorial optimization techniques can solve complex problems?
• Explain how to efficiently solve partial differential equations
• What efficient algorithms can be developed for computational algebraic geometry?
• How do geometric groups behave in various mathematical structures?
• Explain how can complex systems be modeled and predicted using mathematical techniques
• Explore what graph theory algorithms can be applied to real-world network analysis.

The Bottom Line

The list of research topics we have suggested in this blog shows how much more is there to discover in math. Particularly, from basic questions in number theory and algebra to practical applications in machine learning and data science, the math research topics we have recommended above will allow you to explore and learn more. So, for your math research, from our list, feel free to pick any topic that is related to your area of interest and study objectives. Examining the math research topic of your passion will allow you to gain new insights, create new technologies, and solve complex problems. If it is tough for you to conduct an extensive study and prepare a research paper on math topics, then get guidance from experienced mathematicians on our team and finish your task with accurate answers.

Related Post

155 Best Statistics Project Ideas and Topics To Consider

245 Innovative Capstone Project Ideas For Students

190 Impressive Short Story Ideas for Creative Writing

About author.

Jacob Smith

I am an Academic Writer and have affection to share my knowledge through posts’. I do not feel tiredness while research and analyzing the things. Sometime, I write down hundred of research topics as per the students requirements. I want to share solution oriented content to the students.

Comments are closed.

• Featured Posts

180 Funny Speech Topics to Blow the Minds of Audience

200 best ap research topics and ideas, 200 trending group discussion topics and ideas, 255 outstanding world history topics and ideas 2024, 150 unique geology research topics to focus on, who invented exams learn the history of examination, how to focus on reading 15 effective tips for better concentration, what is a rhetorical analysis essay and how to write it, primary school teacher in australia- eligibility, job role, career options, and salary, 4 steps to build a flawless business letter format, get help instantly.

Raise Your Grades with Assignment Help Pro

121+ Maths Project Topics For Students [Updated 2024]

Math isn’t just about crunching numbers or memorizing formulas; it’s a world full of exciting adventures and creative opportunities to discover. High school students often find maths projects both challenging and rewarding. Choosing the right project topics can make all the difference in making maths fun and engaging. In this blog, we’ll explore a variety of exciting maths project topics suitable for students.

What Are The Most Important Topics In Maths?

Determining the “most important” topics in mathematics can vary depending on perspective and application. However, some universally recognized fundamental topics include:

• Arithmetic: Basic operations such as addition, subtraction, multiplication, and division.
• Algebra: Manipulating symbols and solving equations.
• Geometry: Study of shapes, sizes, properties, and space.
• Calculus: Understanding rates of change and accumulation.
• Probability and Statistics: Analyzing data and making predictions based on uncertainty.
• Number Theory: Studying properties of integers and their relationships.
• Linear Algebra: Exploring vectors, matrices, and their transformations.
• Differential Equations: Modeling change and phenomena using equations.
• Combinatorics: Counting and arranging objects.
• Logic: Analyzing arguments and reasoning.

How To Write A Project In Maths?

Writing a project in mathematics involves several key steps:

• Choose a Topic: Select a topic that interests you and aligns with your level of mathematical understanding. Consider areas of mathematics that you find intriguing or relevant to your studies.
• Research: Gather information about your chosen topic from textbooks, academic journals, online resources, and other relevant sources. Understand the background, theories, and applications related to your topic.
• Define Objectives: Make it clear what you want to do with your project. What are your goals? What do you want to show or find out? Say exactly what your project will focus on and what questions or issues you’ll be looking into.
• Develop a Plan: Create a structured plan for your project, outlining the steps you will take to achieve your objectives. This plan should include the methodology you will use, the data you will collect (if applicable), and the analyses you will perform.
• Organize Your Work: Split your project into parts like introduction, reading up, how you did it, what you found, talk about it, and sum it up. Make sure each part makes sense and adds to your project’s overall story.
• Write Your Project: Begin writing your project following the outline and plan you have developed. Clearly explain your topic, provide background information, describe your methodology, present your findings, and discuss their implications. Use clear, concise language and provide relevant mathematical notation and equations where necessary.
• Include Visuals: Incorporate graphs, charts, diagrams, and other visuals to illustrate key concepts, data, and findings. Visual representations can enhance understanding and make your project more engaging.
• Review and Revise: Proofread your project carefully to check for errors in grammar, spelling, and mathematical notation. Ensure that your writing is clear, coherent, and well-structured. Revise as needed to improve clarity and accuracy.
• Cite Your Sources: Acknowledge the sources of information and ideas you have used in your project by providing proper citations. Follow a consistent citation style, such as APA or MLA, as required by your institution or guidelines.
• Finalize Your Project: Once you are satisfied with your project, finalize it by formatting it according to the requirements provided by your instructor or institution. Make sure all sections are properly labeled, and the document is well-presented.

121+ Maths Project Topics For Students: Category Wise

Arithmetic and number theory.

• Exploring the properties of prime numbers.
• Investigating the patterns of Fibonacci sequences.
• Analyzing the divisibility rules for different numbers.
• Exploring the concept of perfect numbers.
• Investigating the properties of odd and even numbers.
• Exploring the concept of modular arithmetic.
• Investigating the properties of triangular numbers.
• Analyzing the distribution of digits on different numbers bases.
• Investigating the properties of palindromic numbers.
• Exploring the concept of amicable numbers.

Algebra and Equations

• Solving systems of linear equations using different methods.
• Investigating the properties of quadratic equations.
• Exploring the solutions to cubic and quartic equations.
• Investigating the properties of polynomial functions.
• Exploring the concept of inequalities and their solutions.
• Analyzing the properties of exponential functions.
• Investigating the solutions to logarithmic equations.
• Exploring the properties of rational functions.
• Analyzing the solutions to radical equations.
• Investigating the properties of complex numbers.

Geometry and Trigonometry

• Exploring the properties of different types of triangles.
• Investigating the properties of polygons and their angles.
• Analyzing the properties of circles and their arcs.
• Exploring the concept of geometric transformations.
• Investigating the properties of 3D shapes and solids.
• Analyzing the properties of conic sections.
• Exploring the concept of similarity and congruence.
• Investigating the properties of trigonometric functions.
• Analyzing the solutions to trigonometric equations.
• Exploring the concept of vectors and vector operations.

Calculus and Differential Equations

• Investigating the concept of limits and continuity.
• Exploring the properties of derivatives and their applications.
• Analyzing the solutions to differential equations.
• Investigating the concept of integration and its applications.
• Exploring the properties of definite and indefinite integrals.
• Analyzing the solutions to differential equations using Laplace transforms.
• Investigating the concept of sequences and series.
• Exploring the properties of power series and their convergence.
• Analyzing the solutions to differential equations using Taylor series.
• Investigating the concept of multivariable calculus and its applications.

Probability and Statistics

• Analyzing the properties of different types of probability distributions.
• Investigating the concept of conditional probability and independence.
• Exploring the properties of random variables and their distributions.
• Analyzing the solutions to problems using combinatorial methods.
• Investigating the concept of expected value and variance.
• Exploring the properties of hypothesis testing and confidence intervals.
• Analyzing the solutions to problems using regression analysis.
• Investigating the concept of sampling distributions and estimation.
• Exploring the properties of statistical tests and their applications.
• Analyzing the solutions to problems using Bayesian methods.

Mathematical Modeling and Optimization

• Investigating the concept of mathematical modeling and its applications.
• Exploring the properties of linear programming and optimization problems.
• Analyzing the solutions to optimization problems using graphical methods.
• Investigating the concept of game theory and its applications.
• Exploring the properties of decision theory and its applications.
• Analyzing the solutions to problems using queuing theory.
• Investigating the concept of network flow problems and their solutions.
• Exploring the properties of dynamic programming and its applications.
• Analyzing the solutions to problems using simulation methods.
• Investigating the concept of stochastic processes and their applications.

Cryptography and Coding Theory

• Investigating the concept of encryption and decryption methods.
• Exploring the properties of different types of cryptographic algorithms.
• Analyzing the solutions to problems using RSA encryption.
• Investigating the concept of digital signatures and their applications.
• Exploring the properties of error-correcting codes and their applications.
• Analyzing the solutions to problems using Hamming codes.
• Investigating the concept of secret sharing schemes and their applications.
• Exploring the properties of block ciphers and their modes of operation.
• Analyzing the solutions to problems using stream ciphers.
• Investigating the concept of quantum cryptography and its applications.

Fractals and Chaos Theory

• Exploring the properties of different types of fractals.
• Investigating the concept of self-similarity and its applications.
• Analyzing the solutions to problems using fractal geometry.
• Investigating the properties of chaotic systems and their behavior.
• Exploring the concept of sensitivity to initial conditions.
• Analyzing the solutions to problems using chaos theory.
• Investigating the concept of strange attractors and their properties.
• Exploring the properties of bifurcations and their applications.
• Analyzing the solutions to problems using dynamical systems.
• Investigating the concept of chaos control and its applications.

Graph Theory and Network Analysis

• Exploring the properties of different types of graphs.
• Investigating the concept of connectivity and its applications.
• Analyzing the solutions to problems using graph algorithms.
• Investigating the properties of planar graphs and their applications.
• Exploring the concept of graph coloring and its applications.
• Analyzing the solutions to problems using matching theory.
• Investigating the properties of directed graphs and their applications.
• Exploring the concept of network flows and their properties.
• Analyzing the solutions to problems using network algorithms.
• Investigating the concept of social network analysis and its applications.

Mathematical Art and Visualization

• Exploring the properties of different types of mathematical art.
• Investigating the concept of symmetry and its applications in art.
• Analyzing the solutions to problems using tessellations.
• Investigating the properties of mathematical knots and their applications.
• Exploring the concept of fractal art and its applications.
• Analyzing the solutions to problems using algorithmic art.
• Investigating the properties of mathematical sculptures and installations.
• Exploring the concept of optical illusions and their mathematical basis.
• Analyzing the solutions to problems using mathematical animations.
• Investigating the properties of 3D printing and its applications in mathematics.

History and Philosophy of Mathematics

• Exploring the history of ancient mathematical civilizations.
• Investigating the contributions of famous mathematicians to the field.
• Analyzing the development of mathematical concepts over time.
• Investigating the philosophy of mathematics and its implications.
• Exploring the concept of mathematical realism and its critics.
• Analyzing the solutions to problems using mathematical intuitionism.
• Investigating the properties of different mathematical axioms.
• Exploring the concept of mathematical proof and its importance.
• Analyzing the solutions to problems using mathematical logic.
• Investigating the role of mathematics in different cultures and societies.

Applications of Mathematics in Science and Engineering

• Exploring the applications of calculus in physics.
• Investigating the role of mathematics in computer science.
• Analyzing the solutions to problems using numerical methods.
• Investigating the applications of statistics in biology.
• Exploring the role of mathematics in chemistry.
• Analyzing the solutions to problems using differential equations in engineering.
• Investigating the applications of linear algebra in data science.
• Exploring the role of mathematics in environmental science.
• Analyzing the solutions to problems using optimization techniques in operations research.
• Investigating the applications of probability theory in finance.
• Exploring the role of mathematics in medical imaging and analysis.
• Analyzing the solutions to problems using mathematical modeling in epidemiology.
• Investigating the applications of graph theory in telecommunications networks.
• Exploring the role of mathematics in robotics and artificial intelligence.
• Analyzing the solutions to problems using mathematical simulations in climate science.

Maths project topics offer an excellent opportunity for high school students to delve deeper into the subject and explore its real-world applications. By choosing a topic that interests them, students can enhance their understanding of mathematical concepts while fostering creativity and critical thinking skills.

Whether it’s exploring Fibonacci sequences in nature, analyzing the mathematics of music, or solving optimization problems, there’s a wealth of exciting project topics waiting to be discovered.

So, roll up your sleeves, unleash your curiosity, and embark on a mathematical journey that’s both challenging and rewarding!

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• Contact Info

DEPARTMENT OF MATHEMATICS

• Undergraduate

Undergraduate Research Projects

Northwestern undergraduates have opportunities to explore mathematics beyond our undergraduate curriculum by enrolling in math 399-0 independent study, working on a summer project, or writing a senior thesis under the supervision of a faculty member. below are descriptions of projects that our faculty have proposed.  students interested in one of these projects should contact the project adviser. this should not be taken to be an exhaustive list of all projects that are availalbe, nor as a list of the only faculty open to supervising such projects. contact the director of undergraduate studies  for additional guidance. these projects are only available to northwestern undergraduates., combinatorial structures in symplectic topology, eric zaslow, symplectic and contact geometry describe the mathematics of phase space for particles and light, respectively.  they therefore are the mathematical home for dynamical systems arising from physics.  a noteworthy structure within contact geometry is that of a legendrian surface, closely related to the wavefront of propagating light.  these subspaces sometimes have combinatorial descriptions via graphs.  the project explores how well the combinatorial descriptions can distinguish legendrian surfaces, just as in knot theory one might explore whether the jones polynomial can distinguish different knots. , prerequisites:  math 330-1 or math 331-1, math 342-0. recommended: math 308-0., complexity and periodicity, the simplest bi-infinite sequences in $\{0, 1\}^{\mathbb z}$ are the periodic sequences, where a single pattern is concatenated with itself infinitely often. at the opposite extreme are bi-infinite sequences containing every possible configuration of $0$'s and $1$'s. for periodic sequences, the number of substrings of length $n$ is bounded, while in the second case, all substrings appear and so there are $2^n$ substrings of length $n$. the growth rate of the possible patterns is a measurement of the complexity of the sequence, giving information about the sequence itself and describing objects encoded by the sequence. symbolic dynamics is the study of such sequences, associated dynamical systems, and their properties. an old theorem of morse and hedlund gives a simple relation between this measurement of complexity and periodicity: a bi-infinite sequence with entries in a finite alphabet $\mathcal a$ is periodic if and only if there exists some $n\in\mathbb n$ such that the sequence contains at most $n$ words of length $n$. however, as soon as we turn to higher dimensions, meaning a sequence in $\mathcal a^{\mathbb z^d}$ for some $d\geq 2$ rather than $d=1$, the relation between complexity and periodicity is no longer clear.  even defining what is meant by low complexity or periodicity is not clear.  this project will cover what is known in one dimension and then turn to understanding how to generalize these phenomena to higher dimensions.   prerequisite: math 320-3 or math 321-3., finite simple groups, ezra getzler, finite simple groups are the building blocks of finite groups. for any finite group $g$, there is a normal subgroup $h$ such that $g/h$ is a simple group: the simple groups are those groups with no nontrivial normal subgroups.  the abelian finite simple groups are the cyclic groups of prime order; in this sense, finite simple groups generalize the prime numbers.  one of the beautiful theorems of algebra is that the alternating groups $a_n$ (subgroups of the symmetric groups $s_n$) are simple for $n\geq 5$. in fact, $a_5$ is the smallest non-abelian finite simple group (its order is $60$). another series of finite simple groups was discovered by galois. let $\mathbb f$ be a field.  the group $sl_2(\mathbb f)$ is the group of all $2\times2$ matrices of determinant $1$. if we take $\mathbb f$ to be a finite field, we get a finite group; for example, we can take $\mathbb f=\mathbb f_p$, the field with $p$ elements. it is a nice exercise to check that $sl_2(\mathbb f_p)$ has $p^3-p$ elements. the center $z(sl_2(\mathbb f_p))$ of $sl_2(\mathbb f_p)$ is the set of matrices $\pm i$; this has two elements unless $p=2$. the group $psl_2(\mathbb f)$ is the quotient of $sl_2(\mathbb f)$ by its center $z(sl_2(\mathbb f))$: we see that $psl_2(\mathbb f_p)$ has order $(p^3-p)/2$ unless $p=2$. it turns out that $psl_2(\mathbb f_2)$ and $psl_2(\mathbb f_3)$ are isomorphic to $s_3$ and $a_4$, which are not simple, but $psl_2(\mathbb f_5)$ is isomorphic to $a_5$, the smallest nonabelian finite simple group, and $psl_2(\mathbb f_7)$, of order $168$, is the second smallest nonabelian finite simple group. (when $\mathbb f$ is the field of complex numbers, the group $psl_2(\mathbb c)$ is also very interesting, though of course it is not finite: it is isomorphic to the lorentz group of special relativity.)  the goal of this project is to learn about generalizations of this construction, which together with the alternating groups yield all but a finite number of the finite simple groups. (there are 26 missing ones called the sporadic simple groups that cannot be obtained in this way.) this mysterious link between geometry and algebra is hard to explain, but very important: much of what we know about the finite simple groups comes from the study of matrix groups over the complex numbers. prerequisite: math 330-3 or math 331-3., fourier series and representation theory, fourier series allow you to write a periodic function in terms of a basis of sines and cosines.  one way to think of this is to understand sines and cosines as the eigenfunctions of the second derivative operator – so fourier series generalize the spectral theorem of linear algebra in this sense.  there is another viewpoint that is useful:  periodic functions can be thought of as functions defined on a circle, which is itself a group.  the connection between group theory and fourier series runs deeper, and this is the subject of this project. moving up a dimension, functions on a sphere can be described in terms of spherical harmonics.  while the sphere is not a group, it is the orbit space of the unit vector in the vertical direction.  thus it can be constructed as a homogeneous space:  it is the group of rotations modulo the group of rotations around the vertical axis.  we can therefore access functions on the sphere via functions on the group of rotations.  the peter-weyl theorem describes the vector space of functions on the group in terms of its representation theory.  (a representation of a group is a vector space on which group elements act as linear transformations [e.g., matrices], consistent with their relations.)  the entries of matrix elements of the irreducible representations of the group play the role that sines and cosines did above.  indeed, we can combine sines and cosines into complex exponentials and these are the sole entries of the one-by-one matrices (characters) representing the abelian circle group.  finally, we will connect spherical harmonics to polynomial functions relevant to geometric structures described in the borel-weyl-bott theorem.  students will explore many examples along with learning the foundations of the theory. prerequisites:  math 351-0 or math 381-0., linear poisson geometry, santiago cañez , a poisson bracket is a type of operation which takes as input two functions and outputs some expression obtained by multiplying their derivatives, subject to some constraints. for instance, the standard poisson bracket of two functions $f,g$ on $\mathbb r^2$ is defined by $\{f,g\} =\frac{\partial f}{\partial x} \frac{\partial g}{\partial y} - \frac{\partial f}{\partial y} \frac{\partial g}{\partial x}$. such objects first arose in physics in order to describe the time evolution of mechanical systems, but have now found other uses as well. in particular, a linear poisson bracket on a vector space turns out to encode the same data as that of a lie algebra, another type of algebraic object which is ubiquitous in mathematics. this relation between linear poisson brackets and lie algebra structures allows one to study the same object from different perspectives; in particular, this allows one to better understand the notion of coadjoint orbits and the hidden structure within them., the goal of this project is to understand the relation between linear poisson brackets and lie algebras, and to use this relation to elucidate properties of coadjoint orbits. all of these structures are heavily used in physics, and gaining a deep understanding as to why depends on the relation described above. moreover, this project will bring in topics from many different areas of mathematics – analysis, group theory, and linear algebra – to touch on areas of modern research., prerequisites: math 320-1 or math 321-1, math 330-1 or math 331-1, math 334-0 or math 291-2., noncommutative topology, given a space $x$, one can consider various types of functions defined on $x$, say for instance continuous functions from $x$ to $\mathbb c$. the set $c(x)$ of all such functions often comes equipped with some additional structure itself, which allows for the study of various geometric or topological properties of $x$ in terms of the set of functions $c(x)$ instead. in particular, when $x$ is a compact hausdorff space, the set $c(x)$ of complex-valued continuous functions on $x$ has the structure of what is known as a commutative $c^*$-algebra, and the gelfand-naimark theorem asserts that all knowledge about $x$ can be recovered from that of $c(x)$. this then suggests that arbitrary non-commutative $c^*$-algebras can be viewed as describing functions on "noncommutative spaces," of the type which arise in various formulations of quantum mechanics. the goal of this project is to understand the relation between compact hausdorff spaces and commutative $c^*$-algebras, and see how the topological information encoded within $x$ is reflected in the algebraic  information encoded within $c(x)$. this duality between topological and algebraic data is at the core of many aspects of modern mathematics, and beautifully blends together concepts from analysis, algebra, and topology. the ultimate aim in this area is to see how much geometry and topology one can carry out using only algebraic means. prerequisites: math 330-2 or math 331-2, math 344-1., simple lie algebras, a lie algebra is a vector space equipped with a certain type of algebraic operation known as a lie bracket, which gives a way to measure how close two elements are to commuting with one another. for instance, the most basic example is that of the space of all $n \times n$ matrices, where the "bracket" operation takes two $n \times n$ matrices $a$ and $b$ and outputs the difference $ab-ba$; in this case the lie bracket of $a$ and $b$ is zero if and only if $a$ and $b$ commute in the usual sense. lie algebras arise in various contexts, and in particular are used to describe "infinitesimal symmetries" of physical systems. among all lie algebras are those referred to as being simple, which in a sense are the lie algebras from which all other lie algebras can be built. it turns out that one can encode the structure of a simple lie algebra in terms of purely combinatorial data, and that in particular one can classify simple lie algebras in terms of certain pictures known as dynkin diagrams. the goal of this project is to understand the classification of simple lie algebras in terms of dynkin diagrams. there are four main families of such lie algebras which describe matrices with special properties, as well as a few so-called exceptional lie algebras whose existence seems to come out of nowhere. such structures are now commonplace in modern physics, and their study continues to shed new light on various phenomena. prerequisites: math 330-2 or math 331-2, math 334-0 or math 291-2., the spectral theory of polygons, jared wunsch, we can study, for any domain the plane, the eigenfunctions of the laplace-operator (with boundary conditions) on this domain: these are the natural frequencies of vibration of this drum head. students might want to read mark kac's famous paper "can you hear the shape of a drum" as part of this project, and there is lots of fun mathematics associated to this classical question and its negative answer by gordon-webb-wolpert.   an ambitious direction that this could possibly head in would be the theory of diffraction of waves on surfaces. in the plane, this is a classical theory, going back to work of sommerfeld in the 1890's, but there's still a remarkable amount that we don't know.  the mathematical story is more or less as follows: a wave (i.e. a solution to the wave equation, which could be a sound or electromagnetic wave, or, with a slight change of point of view, the wavefunction of a quantum particle) is known to reflect nicely off a straight interface.  at a corner, however, something quite interesting happens, which is that the tip of the corner acts as a new point source of waves.  this is the phenomenon of diffraction, and is responsible for many fascinating effects in mathematical physics.  the student could learn the classical theory in the 2d context, starting with flat surfaces and possibly (if there is sufficient geometric background) curved ones, and then work on a novel project in one of a number of directions, which would touch current research in the field., prerequisites: math 320-1 or math 321-1, math 325-0 or math 382-0. more ambitious parts of this project might require math 410-1,2,3..

Department of Mathematics

• Toggle Navigation

Possible Student Research Topics

Projects are listed by faculty member.    Please contact faculty members directly for further information.

Dr. Bourdon:  My research interests lie in arithmetic geometry, which is a field in the intersection of algebraic geometry and number theory. For me, this means studying the arithmetic properties of objects coming from algebraic geometry. In particular, my research involves elliptic curves, which are examples of curves in projective space whose points can be given the structure of an abelian group. They have far-reaching applications, both in theoretical mathematics — such as in the proof of Fermat’s Last Theorem — and in information security where they form the basis of a cryptosystem commonly used to provide secure web browsing.

Coursework in modern algebra is the best preparation for doing research in this area (MTH 321 or MTH 721-722). To get a sense of student research projects I’ve advised, you can check out the theses of some of my former students: Project 1 , Project 2 , Project 3 , Project 4 .

Dr. Gemmer:  Broadly, my research interests lie in analyzing and developing mathematical models of phenomenon in the physical and biological sciences. As an applied mathematician I find significant professional satisfaction studying “toy” models of systems which can yield concrete insights into phenomena observed in Nature. I am also particularly drawn to problems which not only have interesting and important applications but also have the potential to lead to new and deep mathematics. In my work I have developed expertise in calculus of variations, mathematical modeling, applied analysis, continuum mechanics, asymptotic methods, ordinary and partial differential equations and Riemannian geometry. I would be happy to meet with a student to discuss potential projects. Past projects I have mentored include modeling crowd dynamics, modeling the spread of infectious diseases on adaptive networks, brachistochrone problems in inverse square gravitational fields, rare events in stochastic differential equations, modeling adaptation in predator prey systems, and studying the stability of inverted pendulums, i.e. segues. A list of potential and past projects is available at  http://users.wfu.edu/gemmerj/projects.html .

Dr. Jiang:  1.  Network models of infectious disease:  try to investigate the difference between A Markov chain model and a deterministic model. Keywords: Markov chain, rate of eradication, network model, dynamical systems.  2. Multifractal analysis of time series.  Keyword: Holder exponents, Wavelet coefficients, Hausdorff dimension.

Dr. Mason: My main research interests lie at the intersection of algebra and combinatorics, aptly called “algebraic combinatorics”. Specifically, I look for ways to draw pictures and diagrams to represent algebraic concepts and constructions, especially those involving polynomials with some sort of symmetry. These diagrams can often simplify the algebra and pave the way for the discovery of new formulas and theorems. I am also open to exploring projects suggested by students and have mentored projects involving graph theory, game theory, and biological applications of combinatorics. Check out my website https://sites.google.com/wfu.edu/sarahmason/student-research to see examples of some previous student research projects.

Dr. Raynor:  I’m open to working on any topic in the general areas of analysis, differential equations, and differential geometry.  Some areas on which I’ve worked with students before are traffic modeling, free boundary problems, DNA solitary wave modeling, fractals, and ranking theory.

Dr. Robinson: I am interested in many analysis based problems dealing with Differential Equations or Difference Equations. Here, I provide brief introductions to a few of these problems . Any student with a background that includes Multivariable Calculus and Linear Algebra can get started. If you have taken courses such as Ordinary Differential Equations,  Partial Differential Equations, or Real Analysis, then the doors are open to many more problems. The more you know, and the more you are willing to learn along the way, the deeper you can dive.

Dr. Rouse:   Rather than indicate a specific project, I prefer to decide on a project after talking with a student about their interests and background. That said, all the projects I am likely to suggest are in number theory.

Making Mathematics Home | Mathematics Projects | Students | Teachers | Mentors | Parents | Hard Math Café | Research Projects | Research Settings | Mathematics Research Skills | Mathematics Tools | Completed Student Work |